Introdução     Aqui mostramos exemplos de como usar nossa calculadora (Universal Probability Calculator - UPC) em situações em que os dados apresentam uma distribuição normal ou não normal. Também realizamos os cáculos utilizando Excel e Minitab, de modo que o usuário possa entender quão mais simples nossa calculadora é quando comparada com outras.         Resumidamente, em nossa calculadora você não tem que se preocupar se a distribuição é normal ou não, basta colar os dados e clicar no botão "calcular". Já outras em outras ferramentas, você precisa analisar o tipo de distribuição, o que é mais demorado, complexo e cheio de armadilhas que podem induzir o usuário a tomar decisões equivocadas. Exemplo 1 (distribuição normal) Descrição do problema: Suponha que você tenha medido algumas vezes o tempo para ir de sua casa ao trabalho (tabela a seguir). Você descobre que em média leva 53 minutos e deseja saber qual a chance de chegar ao trabalho em menos de 1 hora. Valores medidos em minutos) 52.7 43.5 43.3 59.2 47.8 65.2 38.7 51.7 53.6 54.3 67.9 49.7 51.6 63.8 53.6 Solução usando “Calculadora - UPC”: Primeiro passo é mostrado na figura:   No passo 2, copiar e colar diretamente do arquivo para o campo do site: Após clicar em “Calcular” vê-se que a chance de chegar ao trabalho em até 1 hora (60 minutos) é de 81.9%.  Pronto! Solução usado “Excel”: Excel menu, Data/Dados -> Data Analysis/Análise de Dados -> Descriptive Statistics/Estatística descritiva: retorna a tabela abaixo. Média 53.10165 Erro padrão 2.137853 Median 52.6883 Mode #N/A Standard Deviation 8.279871 Sample Variance 68.55626 Kurtosis -0.36244 Skewness 0.208165 Range 29.1862 Minimum 38.7058 Maximum 67.892 Sum 796.5247 Count 15 Como Kurtosis e Skewness são razoavelmente próximos de zero, podemos assumir que a distribuição é normal, ou pelo menos próxima disto. A amostra tem tamanho 15, relativamente pequena. Deste modo um teste apropriado é o t-test.. 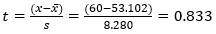Com grau de liberdade 14, temos:        Usando o comando T.DIST(0.833,14,1), temos que a probabilidade de obter um valor de até 60 é de 79.06%.. Solução usando “Minitab”: Inicialmente fazemos o teste de normalidade. No Minitab: Stat-> Basic Statistics -> Normality Test. Para Anderson-Darling e Kolmogorov-Smirnov temos os resultados ao lado, ambos não rejeitando a hipótese nula de normalidade. Sendo assim, é razoável assumir que a distribuição é normal.      Como a amostra é pequena, usaremos o t-test. No Minitab: Calc -> Probability Distributions-> t. Seleciona-se “cumulative probability”, e no campo “input constant” colocamos 0.833 (mesmo t calculado anteriormente para Excel), e obtemos a resposta ao lado, ou seja, a probabilidade de obter um valor de até 60 é de 79.06%. Discussão dos resultados Inicialmente, sobre a fonte dos dados, gerou-se 20 mil valores utilizando-se o software Matlab, função: (randn(20000,1)*5 ) + 50. Assumiu-se que esta é a população. A partir disto coletou-se aleatoriamente 15 valores desta população, listados no enunciado da questão. Resumo dos resultados: UPC-Dunamath Excel Minitab Resposta correta 81.9% 79.06% 79.06% 97.72%   Observa-se que Excel e Minitab retornaram o mesmo resultado, o que é esperado, já que para ambos usou-se a distribuição de Student, com o mesmo parâmetro t. Em ambos assumiu-se que a distribuição é normal, o que é correto, pois os dados da população foram gerados a partir de uma distribuição normal. No entanto os parâmetros de média e desvio usados para calcular t estão significativamente errados, ou seja, a média da amostra é 53.1 e desvio padrão de 8.28, enquanto que a média da população é 50 com desvio de 5. Isto explica o erro na resposta. Outro ponto é que, mesmo usando Excel ou Minitab corretamente, provavelmente o tomador de decisão acreditaria nos 79.06% obtido, pois estas ferramentas não fornecem informações sobre o tamanho da incerteza dos cálculos. O Universal Probability Calculator (UPC) retornou uma probabilidade de 81.9%, um pouco melhor que Excel e Minitab, mas ele também informa que o nível de confiança é baixo (64%), alertando o usuário sobre isto. O UPC, além de calcular a probabilidade de uma forma simples, dá uma estimativa do tamanho da incerteza envolvida. De modo que se o decisor quiser um nível de certeza maior, precisará aumentar o tamanho da amostra. Isto parece ser mais justo com o tomador de decisão. Note que não se está sendo calculado a probabilidade da média da amostra ser menor que 1 hora. Isto é uma pergunta diferente. Exemplo 2 (distribuição não normal) Descrição do problema: Como engenheiro de produto, você está estudando o tempo de vida de um disco rígido de computador. Num experimento, você obteve o tempo de vida em horas de 10 discos, como a seguir: 1988.77 2026.69 2074.94 2018.67 1973.65 1921.29 1941.77 1937.22 1895.03 1942.83   A)     Qual a probabilidade do tempo de vida ser maior que 1900 horas? Solução usando “Calculadora - UPC”: Passo 1: Note que no campo acima poderia ter-se selecionado ≥. Como os valores tratam-se de variáveis contínuas, isto não é relevante.  No passo 2, copiar e colar diretamente do arquivo para o campo do site: Após clicar em “Calcular” vê-se que a probabilidade do tempo de vida ser maior que 1900 horas é de 90.56%. Solução usando "Excel": Menu: Data (Date) -> Data Analysis (Análise de Dados) -> Descriptive Statistics (Estatística descritiva): retirna a tabela abaixo. Média 1972.086 Standard Error 17.48647 Median 1958.24 Mode #N/A Standard Deviation 55.29706 Sample Variance 3057.765 Kurtosis -0.35796 Skewness 0.552605 Range 179.91 Minimum 1895.03 Maximum 2074.94 Sum 19720.86 Count 10 Como Kurtosis e Skewness são razoavelmente próximos de zero, podemos assumir que a distribuição é normal, ou pelo menos próxima disto. A amostra tem tamanho 10, pequena, e considerando-se que a variância da população é desconhecida, considera-se apropriado o t-test. 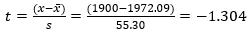Com, grau de liberdade: 9, temos: Usando o comando T.DIST(-1.304,9,1), temos que a probabilidade da vida útil ser maior que 1900 é de 88.8%. 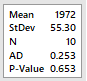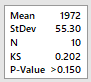Solução usando “Minitab”: Inicialmente fazemos o teste de normalidade. No Minitab: Stat-> Basic Statistics -> Normality Test. Para Anderson-Darling e Kolmogorov-Smirnov temos os resultados ao lado, ambos não rejeitando a hipótese nula de normalidade. Sendo assim, é razoável assumir que a distribuição é normal.    Como a amostra é pequena e a variância da população não é conhecida, usaremos o t-test. No Minitab: Calc -> Probability Distributions-> t. Seleciona-se “cumulative probability”, e no campo “input constant” colocamos -1.304 (mesmo t calculado anteriormente para Excel), e obtemos a resposta ao lado, ou seja, a probabilidade de obter um valor menor que 1900 é de 13.2%. (resultado al lado), ou seja, a probabilidade de ser maior que 1900 é (100-11.2)=88.8%.  B)      Quão certo você está disto? (seu grau de certeza)? Usando UPC-Dunamath, mensagem é mostrado como abaixo: “Estamos 68% confiantes de que o valor verdadeiro está entre 85.56% e 95.56%”. Ou seja, estamos 68% confiantes que o verdadeiro valor seja entre 85.56% e 95.56%. Isto também significa dizer que, se você coletar outras 15 amostras, e fizer isto um número muito grande de vezes, pelo menos 68% das amostras, a probabilidade calculada estará entre 85.56% e 95.56%. Note que Excel e Minitab não disponibilizam esta informação C)      Para aumentar seu grau de certeza na análise, você esperou a conclusão do teste de vida de mais 30 discos (teste complementar) e refez o cálculo de probabilidade com as 2 amostras juntas. Qual a probabilidade do tempo de vida ser maior que 1900 horas e qual a confiabilidade do novo resultado? 1988.77 2026.69 2053.48 2140.11 2132.87 2062.56 1970.53 2164.22 2074.94 2018.67 1982.92 1924.92 2154.11 1788.89 2046.63 2019.41 1973.65 1921.29 1968.29 1753.65 1972.47 2028.2 2000.97 1960.72 1941.77 1937.22 1943.67 1957.47 1909.35 2018.27 2102.17 1695.47 1895.03 1942.83 2063.94 1678.59 1948.96 2050.25 1899.61 2058.53 Solução usando a “Calculadora - UPC”: Passo 1: Passo 2 (colar dados da amostra): Note que no campo acima há mais valores no lado direito, basta percorrer com o cursor do mouse Após clicar em “Calculate” vê-se que a probabilidade do tempo de vida ser maior que 1900 horas é de 85.09%, com 79% de certeza que o valor correto está entre 80.09% e 90.09%. Solução usando "Excel": Excel menu: Data -> Data Analysis -> Descriptive Statistics: Média 1979.302 Standard Error 17.43848 Median 1978.285 Mode #N/A Standard Deviation 110.2906 Sample Variance 12164.02 Kurtosis 1.321178 Skewness -0.90893 Range 485.63 Minimum 1678.59 Maximum 2164.22 Sum 79172.09 Count 40 Kurtosis e Skewness não são próximos de zero, mas nem tão longe. É mais seguro assumir que a distribuição não é normal.. No Excel não há uma forma imediata de tratar distribuições não normais. Uma alternativa em nosso caso, em que Kurtosis e Skewness não estão longe de zero, seria optar pela distribuição de Student com t = (1900-1979.30)/110.29 = -0.719,  Comando Excel T.DIST(-0.719,39,1), resultando em 76.2%.  Uma outra alternativa ainda simples no Excel seria usar a distribuição empírica, como mostrado abaixo.   A tabela de distribuição empírica (EDF) pode ser montada como a seguir: X(i) q < X(i) EDF <x EDF > x 1678.59 1 0.025 0.975 1695.47 2 0.05 0.95 1753.65 3 0.075 0.925 1788.89 4 0.1 0.9 1895.03 5 0.125 0.875 1899.61 6 0.15 0.85 1909.35 7 0.175 0.825 1921.29 8 0.2 0.8 1924.92 9 0.225 0.775 1937.22 10 0.25 0.75 1941.77 11 0.275 0.725 1942.83 12 0.3 0.7 1943.67 13 0.325 0.675 1948.96 14 0.35 0.65 1957.47 15 0.375 0.625 1960.72 16 0.4 0.6 1968.29 17 0.425 0.575 1970.53 18 0.45 0.55 1972.47 19 0.475 0.525 1973.65 20 0.5 0.5 X(i) q < X(i) EDF <x EDF > x 1982.92 21 0.525 0.475 1988.77 22 0.55 0.45 2000.97 23 0.575 0.425 2018.27 24 0.6 0.4 2018.67 25 0.625 0.375 2019.41 26 0.65 0.35 2026.69 27 0.675 0.325 2028.2 28 0.7 0.3 2046.63 29 0.725 0.275 2050.25 30 0.75 0.25 2053.48 31 0.775 0.225 2058.53 32 0.8 0.2 2062.56 33 0.825 0.175 2063.94 34 0.85 0.15 2074.94 35 0.875 0.125 2102.17 36 0.9 0.1 2132.87 37 0.925 0.075 2140.11 38 0.95 0.05 2154.11 39 0.975 0.025 2164.22 40 1 0   Na tabela de distribuição empírica, primeira coluna tem os valores em ordem crescente, a segunda coluna tem para cada valor a quantidade de valores menores ou iguais a ele (coincide com o número da linha), a terceira coluna tem o valor da segunda coluna dividido pelo tamanho da amostra (ou seja, a frequência cumulativa), e finalmente, a quarta coluna tem o complemento da terceira coluna.  Queremos a probabilidade de obter um valor maios que 1900. O valor 1900 está entre o valor das linhas 6 e 7, ou seja, 1899.61 and 1909.35. Desta forma, pode-se dizer que a probabilidade de ser maior que 1900 é alguma coisa entre 82.5% e 85%. Note-se que não há garantias de que o valor correto esteja neste intervalo. Mas como a distribuição provavelmente não é normal, este método permite ter alguma noção da probabilidade desejada. 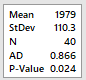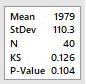Solução usando “Minitab”: Inicialmente fazemos o teste de normalidade. No Minitab: Stat-> Basic Statistics -> Normality Test. Para Anderson-Darling rejeitou-se a hipótese nula de normalidade. Sendo assim, não é razoável assumir que a distribuição é normal. 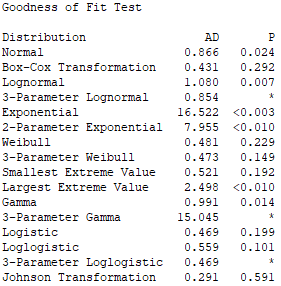Como a distribuição não é normal, precisamos estimar o tipo de distribuição. No Minitab:  Stat > Quality Tools > Individual Distribution Identification. Obtem-se a tabela ao lado, com o teste Anderson-Darling aplicado a vários tipos de distribuição. Em geral, todos aqueles com P<0.05 são imediatamente descartados. Dentre os restantes, escolhe a distribuição com maior valor de P. Em nosso caso seria Johnson Transformation, a seguir Box-Cox Transformation, e a seguir Weibull. Como as duas primeiras são transformações e não distribuição nativas, e não possuem uma forma de uso direta no Minitab, fiquemos aqui com a Weibull. O passo anterior também fornece a tabela a seguir, com os parâmetros de cada tipo de distribuição. Em nosso caso, para Weibull, há 2 parâmetros: 22.30053 (shape) and 2027 (scale). A seguir, no Minitab: Calc -> Probability Distributions->Weibull. Selecionar “cumulative probability”, digitar os 2 parâmetros da distribuição, e no campo “input constant”, entrar com o valor 1900 desejado.  Assim, obteremos a resposta abaixo:                         Como queremos a probabilidade para valores maiores que 1900, temos 1-0.2098=0.7902=79.02%. Ufa, finalmente. Discussão dos resultados: Inicialmente, sobre a fonte dos dados, gerou-se 20 mil valores utilizando-se o software Matlab, função: wblrnd(2042.6,25.8773,20000,1) gerando-se uma população com distribuição Weibull, média 2000.3 e desvio-padrão 97.192. A partir disto coletou-se aleatoriamente os valores desta população, listados no enunciado da questão.                        Para a amostra inicial (N=10): UPC-Dunamath Excel Minitab Resposta corretar 90.56% 88.8% 88.8% 85.82%  Para a amostra estendida: (N=40): UPC-Dunamath Excel (usando distribuição t) Excel (distribuição empírica) Minitab Resposta correta 85.09% 76.2% [82.5% - 85%] 79.02% 85.82%   Para tabela com 10 amostras, observa-se que Excel e Minitab retornaram o mesmo resultado, o que é esperado, já que para ambos usou-se a distribuição de Student (t), com o mesmo parâmetro t. Embora aprovado no teste de normalidade, a distribuição da população é Weibull.  Os parâmetros de média e desvio usados para calcular t são 1972.09 e 55.30 respectivamente, enquanto que a média da população é 2000.3 com desvio de 97.192. Note que embora tenha assumido-se a distribuição errada, o erro da probabilidade foi pequeno, apenas uma coincidência influenciada pela relação entre a média e o desvio-padrão da amostra. Em relação ao caso com 40 amostras, tanto no Excel como Minitab, o teste de normalidade rejeitou a suposição de normal. No Excel, uma forma de ter uma noção do resultado foi usar distribuição empírica, dando algo em torno do intervalo de 82.5% a 85%, mostrando-se ser uma estimativa até razoável. Já no Minitab, depois de todo o trabalho identificando-se a melhor distribuição e seus parâmetros, o resultado até piorou em relação ao caso com 10 amostras, o que é possível, por se tratarem de amostras pequenas, talvez as novas amostras fossem menos representativas da população ou apenas uma coincidência numérica.  Finalmente, observa-se quão complicado estas análises podem ser. Calcular o valor de probabilidade já é complicado, e no final você obtém um resultado cuja incerteza é desconhecida. O Universal Probability Calculator (UPC), torna o cálculo imediato, e ainda lhe dá a informação adicional da incerteza, sem precisar se preocupar com todas as premissas e picuinhas estatísticas, pois tudo isto é analisado pelo nosso algoritmo sem envolver o usuário.